Mysticism, Science ~ or Both?

Originally published October 7, 2012

My husband and I have recently purchased the first two seasons of an intriguing series entitled, Through the Wormhole narrated by Morgan Freeman. This series is a wonderful and fascinating collection of some of the most enduring questions in a number of fields of study. The focus of today’s blog was entitled, “Is There an Edge to the Universe?”

As is not uncommon, the segment really just got me interested and generated more questions than it answered. In addition to this segment we had also watched the thirteen-episode classic, Cosmos, with Carl Sagan. In one of his segments he talks about Pythagoras and the dodecahedron. My sometimes strange mental chemistry began to put some interesting things together. Keeping in mind I am not a mathematician or a physicist, I still thought two concepts developed some 2 ½ millennium apart somehow resonate. I am not the only one.

We will start with a Greek fellow named Pythagoras. He lived somewhere around 582-507 BCE in southern Italy in a town named Croton. At some point he and his followers got into a lot of trouble with the locals and had to flee. What we know of the man’s writings come to us almost exclusively through quotes and references. This makes it a tad difficult to be certain what he contributed and what his disciples contributed. In general, he traveled a great deal when young and when he settled in Croton he formed a philosophical group that studied mathematics as a sacred and esoteric subject that should not be shared with the un-initiated. In the Cosmos episode (Backbone of the Night), Sagan postulates that the Pythagoreans where a contributing factor to squelching the growing innovative and scientific explorations of the Ionians. The whole affair appears to represent an ancient form of religious fanaticism suppressing scientific freedom (ala Sagan).

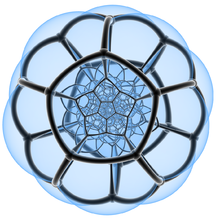
In any case, you may actually recognize the name of this ancient Greek. He is considered, in many ways, the father of geometry. Two things we can attribute to him and his followers: the five perfect solids and the golden ratio. The golden ratio, as it happens, develops mathematically from the formulas used in the formation of the fifth solid: the dodecahedron. The mathematics involved with the dodecahedron produce all sorts of interesting relationships and correlations. It really is no wonder that those who came upon it considered it somehow sacred. The crystal pyrite (fool’s gold) actually forms an imperfect dodecahedron. The Pythagoreans, believing that mathematics formed the foundation of reality, saw something quite magical in the properties related to this particular shape.

We move forward to 1596 CE and we find the intrepid Kepler attempting to explain the paths of the planets by using Pythagoras’ five solids: tetrahedron, octahedron, icosahedron, hexahedron (cube) and dodecahedron. Sadly, this didn’t work out. However, instead of giving up, Kepler used his failure to develop the actual math by which the planetary orbits can be predicted.

Move forward a bit more to the work of Jules Henri Poincaré (1854 – 1912).  Poincaré was a mathematician, theoretical physicist, engineer and a philosopher of science. Among the many, many contributions he made to his fields of study was Poincaré’s homology 3-sphere, or dodecahedral space. I do not have the math to explain what happens in the model; however the work that Poincaré did on the structure led scientists working on the microwave background of the “big bang” to postulate that the universe just might be in the shape of a Poincaré sphere. This is not an interpretation with a general consensus.  Enter the fellow introduced to me in the “Edge of the Universe” episode, Jean-Pierre Luminet of the Observatoire de Paris.

This scientist set out to see if he could determine whether or not the universe had an edge and if so, what was its shape. I need to insert something here.  Scientists working on the “edge of the universe” do not envision an “edge” that one might bounce up against or fall off. What they see is something similar to the world of the old “Space Invaders” video game where if you exit one side of the screen, you would reappear on the opposite side of the screen going in the same direction. Using the model of the dodecahedron, you would exit one of the twelve pentagon-shaped sides and immediately reappear on the opposite side with a bit of a twist. This reminds me a bit of Arthur C. Clarke’s Wall of Darkness about a three dimensional mobius strip.

Back to Luminet. He could tell from the readings of the background microwave noise of the early universe (as we know it) that there were certain sound waves that were “missing.” After much testing he discovered that one particular shape would produce the pattern that we find in those sounds: a common soccer ball, or our ancient friend the dodecahedron. So, maybe Pythagoras was right: the dodecahedron may be the highest and most sacred solid form.

What is really interesting about all of this is that scientist are now looking for ways to reach past that microwave “background noise” and see just what it is that is out there, if anything. Can we tell there is an edge? Are there experiments or astronomical observations that would give us some clues? Are we stuck on the side of a brane? Do we float in an endless series of bubble universes? Will we collide with a neighbor and start the whole thing over again? Is the whole universe composed of singing strings generating all the energy and matter in the universe? Is there anyone else in the vast cosmos that is as excited about learning about the workings of our amazing home as we are?

If you would like to learn more about the history and application of the dodecahedron I have followed this article with a few links to get you started.  In the meantime, what are your favorite mysteries/fascinations with science and the world around us?  Are you drawn to the incredibly small or the incredibly large?  Do you prefer your science in the form of the visible, tangible world around us?  Or do you revel in the abstract philosophy, mathematics and physics of what makes it all tick?  Let me know what you are interested in. You never know what lurks on the shelves of our library!  And remember — “Is it something that we’ve left behind….”

https://math.ucr.edu/home/baez/dodecahedron/

https://physicsworld.com/cws/article/news/2003/oct/08/is-the-universe-a-dodecahedron